Many networks found in nature, such as proteins and molecules, are reproduced with exact connectivity patterns. Relying on mathematical tools such as Bayesian inference and graph theory, along with multiple datasets, we are investigating how nature is able to design networks with exact connectivity patterns.

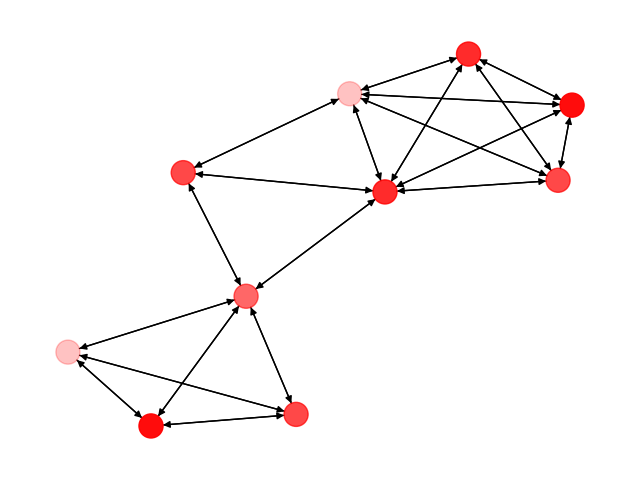
Network reconstruction seeks to reveal the hidden network structure of a system using its node-level dynamics. State-of-the-art methods use Bayesian inference to detect these networks. We are investigating how these methods are biased as a result of the true, underlying structure of the network.

Physical networks are networks which take up volume in 3D-space. We have introduced various measures of link entanglement in these networks, such as the average crossing number and graph linking number. We are now applying these measures to network materials to understand the effect entanglement has on the physical properties of a network.

PageRank is a common algorithm used to rank vertex importance in a graph. We customize PageRank by toggling the amount of backtracking occurring in its underlying random walk. By letting the probability of backtracking go to 1, we introduce ∞-PageRank which can be calculated without approximation. Using ∞-PageRank, we develop a new community detection algorithm.

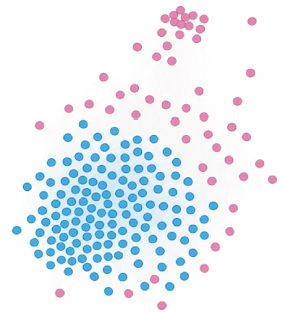
Brain stimulation is an effective therapy for psychiatric illness, however which parts of the brain to stimulate for particular illnesses remains an open question. Using lesion network mapping, we seek to identify stimulation targets which improve depression symptoms in patients in order to create more effective treatment.